2018年中考数学试题延续了2015-2017年试题“稳中求变,变中求新”的特点,在全面考查基础知识、突出对支撑学科体系的重点知识的考查、注重知识的整体性和知识之间的内在联系的基础上,扩大试题的选材范围,以考查数学思维为核心,加强对数学知识形成与发展过程及灵活运用的考查。试卷体现了立德树人,引导教学,服务学生发展的理念。题目素材的选取体现社会主义核心价值观和中华优秀传统文化,增强民族自豪感。设问的方式引导教学以核心概念为抓手、以培养数学能力为目标、以教材中的问题为生长点,帮助学生理解数学本质,学会从数学的角度思考问题、运用数学知识解决数学问题或者实际问题,让学生在数学的学习中有获得感。试题的命制易于学生入手,层次分明,适度综合,体现应用,让不同水平的学生都有充分发挥的空间。
一、关注育人功能 体现积极导向
今年的数学试卷选取合适的素材,将社会主义核心价值观和中华优秀传统文化融入到试题中,发挥试题的育人功能。如第4题以被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST为背景,考查了科学记数法和学生估算的能力,让学生在解决问题的同时了解我国科技发展的现状。
(第4题)被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为7140m2,则FAST的反射面总面积约为
(A)7.14×103m2
(B)7.14×104m2
(C)2.5×105m2
(D)2.5×106m2
如第16题以全球创新综合排名、创新产出排名、创新效率排名为背景,考查学生在图象中读取数据获取信息的能力,让学生感受到我国创新发展水平。
(第16题)2017年,部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22,创新效率排名全球第___
再如第8题以老北京城一些地点的分布图为背景,考查学生对于在不同坐标系下点的相对位置的不变性的理解,同时让学生感悟到中华民族的伟大智慧。
二、关注四基要求 体现数学基础
《义务教育数学课程标准(2011版)》指出:“通过义务教育阶段的数学学习,学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”试题的命制注重对数与代数、图形与几何、统计与概率等基础知识的考查,在考查的过程中,突出对基本技能、基本思想和基本活动经验的考查。在基本技能的教学中,不仅要让学生掌握技能操作的程序和步骤,还要理解其中蕴含的数学原理,如尺规作图的教学不仅要让学生能依据作法准确作出图形,还要求学生利用已掌握的数学原理进行尺规作图的设计,在设计的过程中既体现了不同学生的思维水平,又培养了学生推理论证的能力,如今年试卷中第17题在以往直接写作图依据的基础上,回归到尺规作图的一点,即以某学生设计的“过直线外一点作已知直线的平行线”的尺规作图过程为背景,考查了尺规作图中依据作法作图、推理论证的完整过程。同时,题目设计体现出了对知识掌握的整体性要求,不要把知识割裂开来看,而是从整体上看知识之间的联系性,更好地掌握基础知识。
(第17题)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.

已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ∥l.
作法:如图,
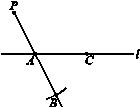
①在直线l上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;
②在直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB= ,CB= ,
∴PQ∥l( )(填推理的依据).
三、关注思维品质 体现教材价值
基于培养数学思维品质的教学,要在充分理解教材、挖掘教材的基础上设计教学活动,培养学生的思维习惯与思维品质。如第7题是一道运用二次函数相关知识解决实际问题的题目,该题取材于课本中的例题,通过赋予其新的实际背景增强了题目的时代气息,题目的解决跳出繁杂的计算,而是利用二次函数图象的对称性再结合题中所给数据,从数与形的角度直接分析推断出二次函数的对称轴,体现了学生灵活运用所学知识解决问题的能力。
(第7题)跳台滑雪是2022年北京冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).下图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为
(A)10m
(B)15m
(C)20m
(D)22.5m
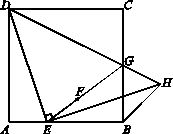
再如第27题是一道几何综合题,该题取材于课本中的习题,通过从运动变化和图形变换的角度对原题进行再设计,挖掘了教材中知识的内在联系,用综合的方法把知识串在一起,发挥了教材促进学生思维发展的功能,同时丰富的试题背景,提供给学生多角度思考问题的机会,提供给学生展示自我的舞台。试题来源于教材,站位又高于教材,难度设置适中。
(第27题)如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.
四、关注教学过程 体现数学本质
数学教学的重要目标之一是让学生亲身经历数学知识形成、发展和应用的过程,积累数学活动经验,感悟数学思想。今年数学试题的设计关注数学学习的完整过程,将学生日常学习活动经验浓缩于试题中,如第24题以函数学习的全过程为背景,考查研究函数的内容与方法,学生在研究几何图形中的各元素之间关系的过程中,经历取点、画图、测量、列表、描点和画函数图象的过程,探究变量之间的关系,并利用建立的函数模型解决问题。引导教学关注有效地数学活动,通过直观地操作活动和多层次地思维活动,从感性认识上升到理性认识,并深化理性认识。
(第24题)如图,Q是AB与弦AB所围成的图形的内部的一定点,P是弦AB上一动点,连接PQ并延长交AB于点C,连接AC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.
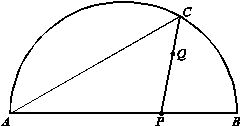
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
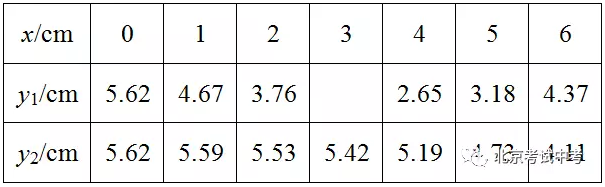
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
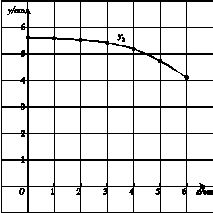
(3)结合函数图象,解决问题:当△APC为等腰三角形时,AP的长度约为 cm.
数据分析是研究随机现象的重要数学技术,是大数据时代数学应用的主要方法。统计教学中要让学生经历完整的统计过程,从数据中提取信息,并利用这些信息说明问题。今年的数学试题在前几年考查数据的收集、整理、描述的基础上,着重考查了对数据的分析和利用数据中提供的信息说明问题,如第25题以抽样调查学生A,B两门课程的成绩为背景,考查了学生对中位数的意义,中位数、平均数、众数在分析数据分布情况的作用,以及样本估计总体的理解,体现学生获取有效信息并进行定量分析的意识和能力。引导教学要关注数学问题的本质,让学生不断积累统计活动经验的基础上,加深理解统计思想与方法。
(第25题)某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A课程成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
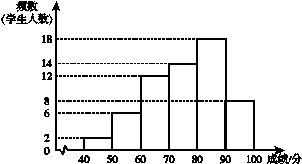
b.A课程成绩在70≤x<80这一组的是:

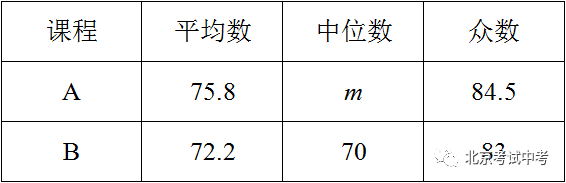
c.A,B两门课程成绩的平均数、中位数、众数如下:
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是 (填“A”或“B”),理由是 ;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过75.8分的人数.
五、关注实践能力 体现应用价值
现实生活中蕴含着大量与数量有关的问题,通过建立数学模型用数学的方法予以解决,体现了数学的应用价值。今年数学试卷扩大试题选材范围,加强与学生生活实际的联系,试题贴近生活,注重考查知识的运用和实践,考查了学生做事能力。如第14题以公交车用时情况为背景,考查学生对于概率意义的理解,体现在解决现实问题而采取策略时概率所起的重要作用;如第15题以租船费用为背景,通过学生探求解决实际问题的最优方案,考查学生运用所学知识分析解决实际问题的能力。
(第14题)从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
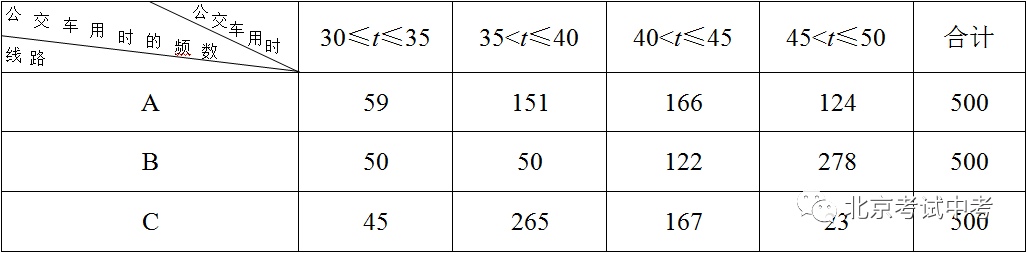
早高峰期间,乘坐 (填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
(第15题)某公园划船项目收费标准如下:

某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为___元.
声明:本文内容来自北京考试中考,由北京中考在线团队-中考升学服务平台(微信公众号:BJ_zkao)综合整理,如有侵权,请及时联系管理员删除。






























